Geometry and load-bearing behavior
The advantages of round shapes compared to rectangular ones
A) The size of all the surfaces of a building (roof, walls, floor), affects the energy sum considerably.
The following explanations are intended to show that spherical shapes have significant advantages in terms of ecology, economy and resistance to strong winds:
1. The shape of the ground surface
The ratio between the floor area of a building to its perimeter is significant for the amount of energy loss (heat/cold transfer) along the foundation.
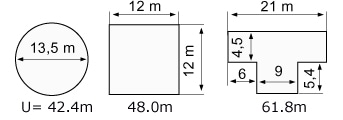
As can be seen in fig. 1, a circle has a smaller perimeter / floor area ratio than a square, rectangle or composite rectangle. With the same surface of 144m² a dome is more efficient, because with circumference of 42,39m it has less perimeter than rectangular floor plans, here in comparison the square with 48,0m and the T-shape with 61,8m.
2. The shape of the building surface
The design of the three-dimensional shape determines the ratio of floor area to surface area. The less surface area or building envelope that needs to be provided, the lower the investment for insulation materials will be.
The less surface area is exposed to the outside, the less energy exchange (heat/cold transfer) takes place.
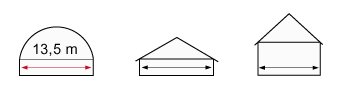
As can be seen in fig. 2, the dome shape exposes less surface than rectangular shapes, with the same floor area.
B) The resistance of a structure to impacting air is responsible for a large proportion of energy consumption.
The amount of energy entering/exiting a house (cold/heat) depends on its insulation and impermeability qualities.
There is a proportional increase in the movement of energy between the inside and outside when winds (cooling) develop. The less wind resistance a form (dome) possesses, the lower the air pressure and thus the loss of the conditioned air will be, which greatly reduces the amount of insulation required.
In addition, the advantages of a round surface and it's lower wind resistance add up. Rectangular shapes form barriers against attacking winds and cause the development of considerable suction effects on the surface of the back of the building (positive and negative wind forces). The combination of these forces causes a greater external absorption and a greater transfer of internal temperature and thus requires more insulation material to counter this effect.
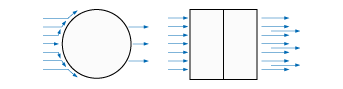
Fig. 3 shows the distribution of the impacting air in a spherical shape compared to a rectangular one.
C) The air circulation within a structure also determines the insulation that is needed to maintain energy efficiency.
As already mentioned, it is on the one hand the sealing and on the other hand the conductivity of the materials used that are decisive for the shell and its performance. The better the insulation properties are, the less energy is needed. There is however a threshold where the values can hardly be improved any further.
The curved shape of a dome house naturally leads to air circulation inside. In a rectangular structure, the warm air rises and, depending on the level, differently warm layers emerge that accumulate just beneath the ceiling. In a dome house, the air rises along the curved wall and then circulates downwards. The heat that flows back into the residual air raises the temperature in the lower part of the room. Since there is less air congestion, which would entail heat loss, it is therefore possible to reduce the insulation requirements. The prerequisite for free air circulation is achieved by an interior layout which is independent of the outer shell stucture, i.e. there are no ceilings or floors supported by the walls to have the room to be like an open gallery.
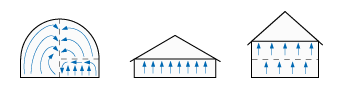
Fig. 4 shows the flow of warm air inside a dome house as well as airflow inside rectangular houses with one or two floors.
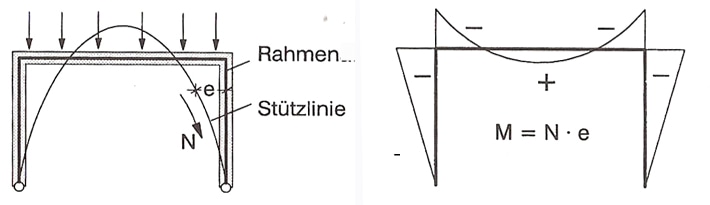
Load-bearing behaviof of arches
Explanation of the difference in the statics of a supporting horizontal beam. Examples of a supporting arch and a beam - from the book: "Domes of all eras - of all cultures" by Erwin Heinle and Jörg Schlaich.
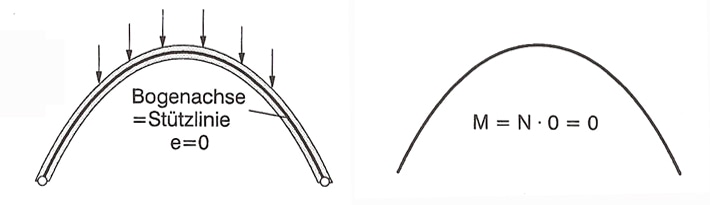
The arc makes more efficient use of the axial forces.
If the axis of an arc follows exactly the support axis belonging to its load, it is actually only stressed by axial pressure forces, which is ideal. The compressive forces thus act exactly in the middle of each cross section, there are no torque variations and an even stress distribution. This means that an arch beam's thickness can be kept constant. The unwanted effect of the dead weight of the structural elements themselves can be overcome. Fig. 5: Bogenachse = Arc axis, Stützlinie = support axis.
Horizontal load-bearing structural designs cannot make use of axial forces
Due to bending forces, the ratio of the thickness of the beam material to the span distance to be bridged is very large. The mass supports, according to the compressive and tensile strength of the material. This structural design therefore has to bear a considerable part of it's own mass. In addition to the stress caused by compressive forces, this must also be taken into account. Fig. 6: Rahmen = frame structure, Stützlinie = Support axis